律曆初階上｜一：律學

基礎知識

槪念

• 調音、律制 tuning 規定音階中各音高的數學方法。律學 研究律制的學問
• 國際標準音高 從古到今不斷升高。有一種方法是：C 爲 $2^8 = 256 hz$，這箇數字非常優美，所以稱爲「物理學高度」，五度相生律 $A1 = 256 × \frac{27}{16} = 432$，純律 $A1 = 256 × \frac{5}{3} = 426.667$
• 音程 兩箇音的距離。音程的命名規則：一度、四度、五度、八度完全和諧，因此前加「純」perfect，一度、四度、五度、八度只有減 diminished –純–增 augmented，其餘的二三六七度只有減–小 minor –大 major –增。例如，1–♭3 是小三度，2–♯6 是增五度。大音階中，每箇音和第一箇音第一音級的距離爲「純」或「大」，如 C-D 是大二度，C-F 是純四度
• 生程 generator 生律所用到的音程。比如三分損益法的生程就是純五度 $\frac{3}{2}$
• 轉位 生律次數相同，方向相反，相加等於八度。轉位音程換算規則：增─減、大─小、純─純。如增二度–減七度，大三度–小六度，如 2–6 爲純五度，6–2 爲純四度
• 音差 comma 某種細微的音程差別，如最大音差 comma maxima, Pythagorean comma、普通音差或合音差 syntonic comma
• 限 limit 某種調音的生程頻率比的分子分母分解質因數，所得最大的質數。比如五限純律之所以是五限，因爲三種生程 $\frac{3}{2}\space \frac{5}{4}\space \frac{6}{5}$ 分解質因數，最大是 5
• 純律 just intonation 有廣義狹義之分，廣義指頻率比爲簡單整數之比的調音，用這種方法調音的音程稱正音程 just/pure intervals。之所以和諧，是因爲這樣產生的和弦處於一箇泛音列中，很接近一箇單音。例如頻率比爲 1 和 $\frac{3}{2}$ 的兩箇音，$\frac{3}{2}$ 的泛音列是 1 的泛音列的子集。而狹義的純律指五限純律
• 調律 temperament 爲了某種特定的音樂實踐，將一部分有缺陷的音程轉移到相對完美的音程中；也可以說，調和了某種音差的調音是調律。純律與調律是相對而言的概念。在一箇只有 12 音的鍵盤中，必須在三六度的協和程度、四五度的協和程度、自由轉調等因素中權衡，例如四分音差折中律犧牲了純五度的協和，實現了大三度的協和，十二等程律犧牲了三六度的協和，取得了移調的自由。根據小樣本調查，大部分現代人能聽出四分律和十二等程律的區別，認爲四分律聲音融合較差，一些音程較突兀。
• 和弦 chord 組合在一起的多箇不同音高的音。舉例：
  • 大三和弦：大三 + 小三 = 純五，如：1-3-5
  • 小三和弦：小三 + 大三 = 純五，如：2-4-6
  • 大七和弦：大三 + 純五 = 大七，如：1-3-7
  • 小七和弦：小三 + 純五 = 小七，如：2-4-1
• 命名：根據生律順序，以 F C G D A E B 爲一箇單位，依次排下來就是 ♭F ♭C ♭G ♭D ♭A ♭E ♭B F C G D A E B ♯F ♯C ♯G ♯D ♯A ♯E ♯B⋯⋯

發音原理

樂器根據發音原理可分爲五類：

• 弦振 弦長和頻率比互爲倒數
• 氣振 運用超吹的方法，可以使倍音轉化爲基音類似弦振的泛音。管子分爲開管與閉管，開管兩端敞開，閉管有一端封閉，同樣長度，開管比閉管高八度。氣柱長度比管子長度略長，因而需要進行管口校正
• 體振 鑼、鈸、鐘、音叉等
• 膜振 鼓等。膜振不能發出整數倍的音，因而音高模糊不定

弦振截止之處稱爲節點，弦振中心稱爲腹點。一根弦除了整體振動，還會分節振動，同時包含基音、二倍音 $\frac{3}{2}$、三倍音 $\frac{4}{3}$……人爲迫使弦分節振動，就能發出泛音。這一系列音就稱爲泛音列 Harmonic series。基音上方的其他音叫上方分音 upper partials 或泛音 overtones。除了音叉，大多數樂器發出的每箇音都是基音和上方泛音的複合音。

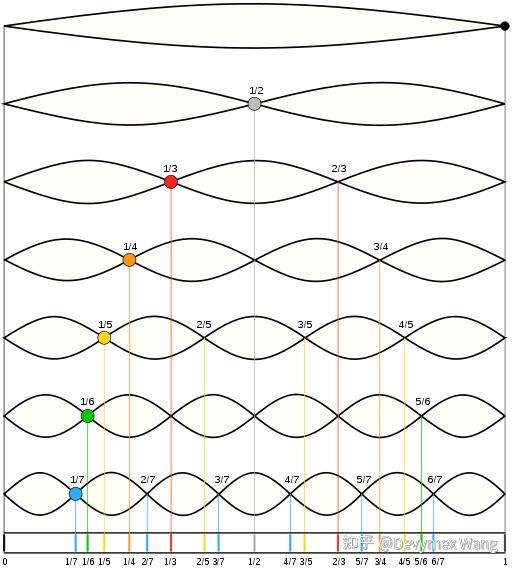
音律計算法

只有頻率比纔能表示聽覺上的音程大小，因此計算時是以「乘積」爲基準，而不是簡單的「乘法」，涉及乘積的運算爲指數、對數、開方。用對數把頻率比化爲音程，得到音分，就可以進行簡單的加減運算了。計算音律時一般限於一箇八度之內，要把頻率比歸到 1–2 之內。

兩音程之和的頻率比 ＝ 兩音程頻率比相乘，兩音程之差的頻率比 ＝ 兩音程頻率比相除。如，純四度和正大三度之和爲純律大六度，其頻率比爲 $\frac{4}{3} × \frac{5}{4} = \frac{5}{3}$。一般不用頻率比表示音程，而用音程値。音程値有四種：對數値、八度値、音分値、平均音程値。

• 八度値 $八度値 = log_{2}{頻率比}$。一箇八度的八度値 = $log_{2}{2} = 1$。上圖爲八度値函數圖像。
• 音分 符號 ¢ 。把一箇八度分爲 1200 份，卽 $音分 ＝ 1200 × 八度値$ ，等程律半音的音程爲 100 音分。1 音分頻率比 = $\sqrt[1200]{2} ≒ 1.0005777895$

音程表

表一：五度律、五限七限純律

除了 C D F G 是共用，其他加了上下線的都是純律。「共有」指五度律、純律共有的音；「純律」指五限純律；「七限」指七限純律。徽位是直接用程序把弦長比轉換爲徽位。純律只列骨幹音，其他的見音系網。

表二：十二十九等程律、四分三分折中律

等程律的頻率比是我選擇的漸進分數。

用音分加一下就知道，五度律、純律是增四，五度律是三箇大全音，純律是兩箇大全音 + 純律小全音；十二等程律的三全音是增四減五；十九等程律小三全音是增四，大三全音是減五。

五度律 三限純律

西方：五度相生律

畢達哥拉斯調音 Pythagorean tuning 是西方第一箇理論化的調音系統。

生律法

五度律用兩種生律方法：

• 上生、隔八相生、純五度：一直乘 $\frac{3}{2}$
• 下生、隔六相生、純四度：一直乘 $\frac{4}{3}$

用到的生程是 $\frac{3}{2}\space \frac{4}{3}$，最大質因數是 3，所以本質上是三限純律。

五度律面臨不能周而復始的問題，生 12 次後多出 23.5 音分，不能回到始發律，稱最大音差、畢氏音差。

$1\overbrace{×\frac{3}{2}×\frac{3}{2}\dots×\frac{3}{2}}^{12} = \frac{531441}{524288} = 𝄪B, 23.5¢$

半音與全音

五度律的半音分兩種，五度律小半音和大半音。

• 小半音/自然半音：向下生 5 次，$\frac{2}{3}^5 × 2^3 = \frac{256}{243}, 90¢$
• 大半音/變化半音：向上生 7 次，$\frac{3}{2}^7 × \frac{1}{2}^4 = \frac{2187}{2048}, 114¢$
• 大全音：向上生 2 次，$\frac{3}{2}^2 / 2 = \frac{9}{8}, 204¢$
• 大全音 = 大半音 + 小半音
• 最大音差 = 大半音 - 小半音 = 向上生 12 次，$\frac{531441}{524288}, 23.5¢$

例如：D 小半音 ♭E 最大音差 ♯D 小半音 E

音階

五度律大音階：向上生 5 次，向下生 1 次。

五度律自然小音階：向上生 2 次，向下生 4 次。

關於音階的產生原理，可以看好和弦視頻 小调的三种模式：自然／和声／旋律小音阶！。

中國：三分損益法

生律法

以長度進行計算，長度是頻率的倒數。三分損一：$× \frac{2}{3}$，三分益一：$× \frac{4}{3}$，一損一益交替進行。這其實只是爲了歸到一箇八度之內，本質都是頻率比 $× \frac{3}{2}$ 的向上純五度相生。正統的三分損益法是先損，這樣黃鐘就是最低的一箇音。若先益一，則林鐘徵在黃鐘宮之下，稱「下徵」。

黃鐘 81損
林鐘 54益
太簇 72損 南呂 48益 姑冼 64損 應鐘 $42\frac{2}{3}$益
蕤賓 $56\frac{8}{9}$益
大呂 $75\frac{23}{27}$損 夷則 $50\frac{46}{81}$益
夾鐘 $67\frac{103}{243}$損
无射 $44\frac{692}{729}$益
仲呂 $59\frac{2039}{2187}$損
清黃鐘 $82\frac{55105}{524288}$

長度由長到短排列：黃鐘、大呂、太簇、夾鐘、姑洗、仲呂、蕤賓、林鐘、夷則、南呂、無射、應鐘。

京房六十律

爲了解決不能旋相爲宮的問題，京房前 77–前 37 年把 12 律延伸到了 60 律，算得色育第五十四的頻率比是 $1\frac{40432553845953101497907}{19342813113834066795298816}$，音分 $3.61504587$，稱爲「京房音差」。

陳應時先生認爲：

• “京房六十律”没有附会“八卦”。据后汉书·律历志记载，京房在创制“六十律”时，是严格按照三分损益法生出来的，而不是附会八卦的产物。倘若京房眞的是附会八卦，则必然是按八卦的分卦法搞成“八八六十四律”。因有些版本的前汉书记写的是“分六十卦”，所以京房六十律就由此被扣上“附会六十卦”的帽子。但八卦是“太极、两仪……”等以倍数连续分卦的，故八卦中不存在“六十卦”之说。此“六十卦”者，应是“六十四卦”之误。
• “京房六十律”不是凑整数。京房律的第五十四律“色育”时，基本已回到了第一律的“黄钟”，他之所以又继续生了“谦待、未知……南事”等六律，陈先生认为他不是为了凑六十整数，而是要达到“自冬至始、及冬至而复”那样的“还相为宫”。这里的“宫”，不是黄钟一个音，而是黄钟至应钟七声所组成的一“均”，故“色育”之后还要再生六律，才能形成与黄钟均七律各相距“一日”的“色育均”。
• “京房六十律”不是宣传迷信的工具。陈先生指出，“京房六十律”的每一律或代表一天，或代表五天、六天、七天等，并不是拥护律历相通的迷信。经音分计算可知，京房所命名的“一日”，正是我们今天所说的“京氏音差”3.615 音分。若将十二律部之间的天数相加，则可以依次得出 31 天、30 天，31 天、30 天……。这也正是今天三分损益十二律中“大半音”、“小半音”的最好解释。

錢樂之三百六十律

錢樂之約 445 年算到了第 360 箇，頻率比是 $1\frac{2060690258392248843304477540277082812788834594155180613917026572029891923938119300378593263340370864556746297173442590623570356295738742074634926562078835993228279321355}{1932268761508629172347675945465993672149463664853217499328617625725759571144780212268096883290961288981231808015751088588682539330521493827871454336733540374348490407411712}$，分母達到了 172 位之巨，音分是 $1.84531067$，已經相當接近了，但是沒有任何實用意義。這箇數字是我用電腦算的，京房錢樂之當時肯定不會算那麼精確。

五限純律 七限純律

五限純律

用純五度 $\frac{3}{2}$、正大三度 $\frac{5}{4}$、正小三度 $\frac{6}{5}$ 三種音程關係生律的純律，稱五限純律或五限調音 5-limit just intonation, 5-limit tuning，也是一般所說的純律。畢氏調音的大三度 $\frac{81}{64}$、小三度 $\frac{32}{27}$ 是不協和的，這妨礙了音樂家使用三和弦。中世紀後期，音樂家意識到可以略微調節某些音的音高，來達成協和。例如，将 E 減少一箇合音差 $\frac{81}{80}$，減爲 $\frac{80}{64} = \frac{5}{4}$，則 C–E 和 E–G 就可變爲正音程。五限純律的不足之處在於，2-6 的五度並不和諧，是窄五度 $\frac{40}{27}$。

音系網

五限純律按照大三和弦生律，當構成大三和弦 C-E-G、F-A-C、G-B-D 時，用五限純律最和諧小三度 + 大三度 = 純五度，純五度 + 大三度 = 大七度。

用這種方法一直生律，將純五放在本行，大三放在上方，小三放在下方，就能構成純律音系網。右上比左下高大三度，右下比左上高小三度，下一行的同名律比上一行高一箇合音差，右方比左方高純五度。

需要注意的是，一箇音階選取不同的音時，各音需要在圖中有所連結。

半音與全音

• 合音差、普通音差 ＝ $\frac{81}{80}, 21.5¢$。加下劃線表示比五度律同名音低一箇合音差，兩箇下劃線表示低兩箇合音差，上畫線則是高一或兩箇合音差
• 升降差 diesis = 大半音﹣小半音 = 3 個正大三度與纯八度之差 = $\frac{128}{125}, 41.059$
• 大升降差 major diesis = 4 個正小三度與純八度之差 = $\frac{648}{625}, 62.565¢$
• 小半音 = 正大三度 - 正小三度 = $\frac{25}{24}, 71¢$
• 大半音 = 純四度 - 正大三度 = $\frac{16}{15}, 112¢$
• 純律小全音 = 小半音 + 大半音 = 正大三度 - 大全音 = $\frac{10}{9}, 182¢$
• 大全音同五度律

C 大調中，C–D 的兩箇半音我們選 ♯C 和 ♭D，爲何選這兩箇而不選 ♯C 和 ♭D呢？一箇訣竅：在音系圖上找連接次數最少的。可以算出 C–♯C 頻率比 25/24、71 音分純律小半音，♭D 頻率比 16/15，112 音分純律大半音。

例如：D 小半音 ♯D 升降差 ♭E 小半音 E 。純律 1–2 爲大全音，2–3 爲小全音；1–5 純五度，2–6 窄五度；3–6 純四度，6–2 寬四度。

音階

扎利諾 Gioseffo Zarlino 在 16 世紀晚期創造了第一箇七音純律自然音階，其中包括完美五度、正大三度和正小三度。純律大音階 E、 A、 B 都比五度律低一箇合音差。

純律自然小音階在五度律純五度基礎上加入正小三度而成。純律小音階 E、A、B 都比五度律高一箇合音差。

性能

在五限純律對稱音階中，2 和 ♭7 互爲轉位，非對稱音階則不能轉位。五限非對稱系統有 9 箇完美五度、8 箇正大三度、6 箇正小三度，以及 2 箇不純五度 D–A $\frac{40}{27}$、3 箇不純小三度 D–F $\frac{32}{27}$，這使得它只能在狹窄的調性內轉調。非對稱有 14 箇狼音程，而對稱只有 12 箇。而七限純律除了有五限純律的這些音階外，還有一箇非對稱音階。表格空白表示同前。

七限純律

七限純律與五限純律有 $\frac{225}{224}, 7.71¢$ 音差，叫七限音差或奇觀差 Septimal kleisma, marvel comma，我簡稱限差。有降號的音，七限比五限高一限差；升號比五限低一限差。下爲音系網，獨家製作。黑色是五限純律音系網，紅綠色是七限純律。讀者可以腦補成一幅三維圖像，綠色表示比五限低一個限差，在黑色後面；紅色表示比五限高一個限差，在黑色前面。其他規則與五限圖相同，向右爲純五度，向右上爲正大三度，向右下爲正小三度。

總的來說，七限的七聲與五限完全相同，不同之處在於有升降號的音，具體見音程表。綠色部分的節點是 $\frac{7}{5}$ ，紅色部分節點是 $\frac{5}{7}$，其他音都是從這 2 個節點中生出的。

七限有如下音比五限數字更簡單、更協和：

調律

在越來越豐富的音樂應用中，五度律和純律往往限制了作曲家的表達，因此需要在這兩種律制中進行調和，產生新的律制，最廣為熟知的就是中庸全音律。

需要說明的是，平均律 equal temperament 最好翻譯爲等程律，中庸全音律 meantone 最好翻譯爲平均律，畢竟從英語來看，mean 指平均，equal 指相等。但爲了避免和現在所說的平均律混淆，我們借用陳長林先生的名詞，將 meantone 譯爲折中律，或者調和律。之所以叫中庸全音律，是因爲全音在純律大小全音之間。

折中律 中庸全音律

四分之一音差折中律是折中律的代表，把 4 個純五疊加，變為正大三 5/4。16 世紀以後，三和弦使用變多。五度律的 3 是 1 上生 4 次的 $\frac{81}{64}$，不如 $\frac{5}{4}$ 和諧，爲了解決這箇問題，每生一次，減少合音差的 $\frac{1}{4}$，這樣生 4 次就能得到 $\frac{5}{4}$。列出方程 $\frac{5}{4} = \frac{x^4}{4}$除以 4 是爲了歸到一箇八度內，解得 $x = \sqrt[4]{5} ≒ 1.495349$，卽四分律的純五度頻率比，不如完美五度和諧，但生 4 次後能得到完全和諧的大三度。還有下生純四度，五度律 ♭A 是下生 4 次的 $\frac{128}{81}$，不如純律小六度 $\frac{8}{5}$ 和諧，於是每生一次增加 $\frac{1}{4}$ 音差。列出方程 $\frac{8}{5} = \frac{x^4}{2}$，解得 $x = \sqrt[4]{\frac{16}{5}} ≒ 1.337481$，卽純四度頻率比。之所以利用小六度解下生方程，因爲小六是大三的轉位，正如純四是純五的轉位。四分律利用上升純五和下生純四各 12 次來生律。四分律上生 9 次的♯D 270¢–下生 2 次的♭B 1007¢ 相距 737¢，構成狼音程 wolf interval，距離純律的 702¢ 非常遠。

三分之一音差折中律是另一種典型的折中律，把 3 個純四疊加，變為正小三度 $\frac{6}{5}$。畢氏小三度是下生 3 次的 $\frac{32}{27}$，不如正小三度和諧，爲了實現和諧的小三和弦，每生一次，減少合音差的 $\frac{1}{3}$。列出方程 $\frac{6}{5} = \frac{x^3}{2}$除以 2 是爲了歸到一箇八度內，解得 $x = \sqrt[3]{\frac{12}{5}} ≒ 1.338866$，卽純四度頻率比，不如純律的 $\frac{4}{3}$ 和諧，但能得到完全和諧的小三度。從音程表可見，三分折中律和十九等程律的每箇音都相當接近，直接純四度下生 19 次就得到整箇音階。音程名我還不確定，暫時照搬十九等程律，希望我沒想錯，應該不需要上下各生 12 次。

新律

何承天造元嘉曆者造新律：

律呂相生，皆三分而損益之。先儒推十二律，從子至亥，每三之，凡十七萬七千一百四十七，而三約之，是爲上生。故漢志云：三分損一，下生林鍾，三分益一，上生太蔟。無射既上生中呂，則中呂又當上生黃鍾，然後五聲、六律、十二管還相爲宮。今上生不及黃鍾實二千三百八十四，九約實一千九百六十八爲一分，此則不周九寸之律一分有奇，豈得還爲宮乎？

三分損益法本來是這樣的：

何承天將黃鐘長度定爲 177147 這一最小公倍數，到了八度黃鐘，弦長少了 $2384\frac{1}{3}$，黃鐘九寸，一分 = 1968，則相差一分多。於是他將 $2384\frac{1}{3}$ 等分爲 12 份，每律加上一份，可得：

下爲新律 12 律音分：100.734 200.407 302.786 401.588 505.41 603.416 700.642 805.782 902.362 1008.593 1104.583 0，可與十二等程律比較一下。但是新律只是表面上實現了黃鐘還原，並不能眞正自由旋宮，這也提示我們，在傳統三分損益法基礎上加以調整，並不是新律制的出路。

他又說：

凡三分益一爲上生，三分損一爲下生，此其大略，猶周天斗分四分之一耳。京房不思此意，比十二律微有所增，方引而伸之，中呂上生執始，執始下生去滅，至於南事，爲六十律，竟復不合，彌益其疏。班氏所志，未能通律呂本源，徒訓角爲觸，徵爲祉，陽氣施種於黃鍾，如斯之屬，空煩其文，而爲辭費。又推九六，欲符劉歆三統之數，假託非類，以飾其說，皆孟堅之妄矣。

可見何承天並不喜歡像一般學者那樣，將音律與其他系統牽合起來。在何承天的思考方式中，三分損益一只是舉約數而言，是古人的模糊化表述，正如都說週天度是 $365\frac{1}{4}$ 度，而元嘉曆實際上是 $365\frac{75}{304} ≒ 365.24671$ 度。何承天認爲只有自己發現了自古相承的三分損益法的眞諦，京房、班固等人都只是南轅北轍，徒費功夫。這一隱藏的思想脈絡似乎未引起音樂史研究者的關注。

三五調和律

三五調和律是陳長林先生提出的用於解決泛音同音不同高問題的琴律，有兩種。何承天新律調和的是五度律系統內部旋相爲宮的問題，而中全律、三五調和律解決的是五度律和純律之間的問題。大意爲，在三分損益基礎上，將合音差平分爲 4 份，每份 5¢。三五調和律沒有標準的品弦法，是在準法品弦法基礎上，靠聽覺來調得稍微低一些。

等程律

在折中律上更進一步，將一箇八度的每箇音等分，就是等程律，等程律當然也是調律。十二等程律是現在通行的律制。說到等程律，經常提及的兩部著作是萬曆十二年 1584 朱載堉律呂精義、1585 西蒙·史蒂文 Simon Stevin，朱載堉提供了精確的計算方法，而西蒙的方法不太精確，兩者是獨立發生的。

几个世纪以来，欧洲使用了各种各样的调音系统，包括十二等程律 12-TET，以及平均律律 meantone temperament 和优律 well temperament。最后，十二等程律胜出，这使得对称调性 symmetrical tonality 和多调性 polytonality 的新风格得以出现，无调性音乐，如用十二音技术或序列主义创作的音乐，以及爵士乐至少是它的钢琴部分得以发展和繁荣。

十二等程律

產生法

五度律向上生 12 次，與 C 相差最大音差 23.5 音分，現在若把每次相生的純五度都減小最大音差的 $\frac{1}{12} ≒ 2¢$，就可以回到 C 了。每次生律的頻率比爲 $\sqrt[12]{2} ≒ 1.059463$。

半音

由於所有半音全都相等，所以等程律有異名同音現象：C=♯B 𝄫D，♯C=𝄪B ♭D，D=𝄪C 𝄫E，♯D=♭E 𝄫F，E=𝄪D ♭F，F=♯E 𝄫G，♯F=𝄪E ♭G，G=𝄪F 𝄫A，♯G=♭A，A=𝄪G 𝄫B，♯A=♭B 𝄫C，B=𝄪A ♭C。

音階

自然大音階：

自然小音階：

新法密率

現在我們直接用電腦算 $\sqrt[12]{2}$ 就可以了，那麼朱載堉的新法密率是怎麼計算的呢？如下圖，設黃鐘正率長度爲 1 尺，黃鐘倍率爲 2 尺，依次作圓、方、圓，據勾股定理卽可得，中間方的長度爲 $\sqrt{2}$。這正是十二律中位於正中的蕤賓的長度。這是朱載堉絕頂聰明的發明，將算術與幾何聯繫起來。問題轉換成首項 2、末項 1、中項 $\sqrt{2}$、公比 $\sqrt{2}$ 的等比數列。

造率始於黃鐘，必先求蕤賓者，猶冬夏二至也；次求夾鐘及南呂者，猶春秋二分也。始於黃鐘者，履端於始也；中於蕤賓者，舉正於中也；終於應鐘者，歸餘於終也：律與曆一道也。

朱載堉有很鮮明的律曆合一的思路，此處算律將律與曆聯繫起來，而在他的黃鐘曆中，將曆與律聯繫起來。之所以說蕤賓猶如冬至夏至，因爲古曆的日躔表太陽變速運動表以二至爲起始，冬至到夏至和夏至到冬至用一張表；之所以說夾鐘南呂猶如春分秋分，因爲冬至到春分、春分到夏至，或者春分到夏至、夏至到秋分兩邊對稱。

求得蕤賓後，再以蕤賓爲端點，求得 $夾鐘南呂 = \sqrt{10 蕤賓}$。接著求 $應鐘 = \sqrt[3]{100 南呂}$。中國古代有增乘開方術，開平方開立方都不成問題。不過增乘開方術到朱載堉的時候已經失傳，他用的其他數學方法，可以參看參考文獻。朱載堉還列出了各係數的近似展開以方便計算，例如純五度爲 $\frac{500000000}{749153538}$。

十九等程律

將一箇八度平分爲 19 份，每箇音 $\frac{1200}{19} ≒ 63.1579¢$。十九等程律與十二等程律都有各自的異名同音音，十九等程律有：♯E = ♭F、♯B = ♭C、𝄪C =♭D 等等。

從音程表的誤差中可見，十九等程律提供了適應古典和聲的純五度、大小三度、大小二度及其轉位。大小三度 十九比十二更接近純律。純五度 十九沒有那麼平滑。全音 十九、十二的全音都介於純律大小全音之間，即中庸全音。半音 十九有兩種半音，聽感完全不同。② 比較協和，其轉位 ⑰ 近似十五倍泛音，是一箇穩定的大七度；① 極不協和，傾向性極強，作爲導音能夠提供強大的屬功能。三全音 十九等程律有兩種互爲轉位的大小三全音。其他 ④ ⑦ ⑫ ⑮ 是古典和聲中不存在的音程，這些聲響對十二等程律耳朵是高度陌生的，但它們所近似的頻率比也都能在十五倍泛音以下找到。這說明十九等程律提供了更豐富的和聲性能，在當代音樂中意義深遠。

二十四等程律

阿拉伯音樂家數學家 Michael Meschāqa1800–1888在論希哈卜的音樂藝術中提出二十四等程律，將各律之間分爲 50¢，以適應阿拉伯各種音階的特殊需求。阿拉伯有 17 種音階，除了全音和半音，還有 50、150、250¢的微分音。

規則調律理論

最後一節是進階內容，跳過无妨。

規則調律理論 regular temperament theory (RTT) 是對音程的數學模型化。該理論把音程理解爲一箇向量空間，利用線性代數，來選擇音高。一個調音中，通常用一個生程充當週期 period。週程 pergen 卽週期、生程的合稱。例如：四分折中律是 2 秩調律，純八度是週期，純五度是生程，寫作 $(P8, P5)$。

用狄拉克符號 $⟨ ]$ 和 $[ ⟩$ 來表示，中間的數字與從小到大排列的質數有關，前者用於某調律的定義，後者用於某音程的定義。前者例如：十二等程律是五限的，用到了 2 3 5 倍音來生程，寫作 $ ⟨12\space19\space28]$ ，它的 2/1 用 12 步生程，3/1 用 19 步，5/1 用 28 步。後者則是對頻率比分解質因數，取其指數爲向量，例如： $\frac{49}{48} = 2^{-4} × 3^{-1} × 5^0 × 7^2 = [-4\space-1\space0\space2⟩$。

兩種符號可以合併計算，如：$\frac{9}{8} = 2^{-3} × 3^2 = [-3\space2\space0⟩$，那麼在十二等程律中生出 $\frac{9}{8}$ 需要幾步？直接用矩陣計算即可，$ ⟨12\space 19\space 28\mid -3\space 2\space 0⟩ = 12 × (-3) + 19 × 2 + 28 × 0 = 2$。而 $\frac{10}{9} = 2^1 × 3^{-2} × 5^1 = [1\space -2\space 1⟩$，$ ⟨12\space 19\space 28\mid 1\space -2\space 1⟩ = 2$，說明在十二等程律中 $\frac{10}{9}$ 和 $\frac{9}{8}$ 沒有區別，都是 2 步生出來，該律調和的是 $\frac{9}{8} / \frac{10}{9} = \frac{81}{80}$ 的音差。檢驗一下，$\frac{81}{80} = 2^{-4} × 3^4 × 5{-1} = [-4\space 4\space -1⟩$，而 $ ⟨12\space 19\space 28\mid -4\space 4\space -1⟩ = 0$，步數爲 0，說明就是這種調律要調和的音差。

用這種規則來介紹一些音差：

• 最大音差 $\frac{531441}{52488} = [-19\space12⟩$
• 合音差 $\frac{81}{80} = [-4\space4\space-1⟩$
• 分裂差、亥氏差 schisma，最大音差與合音差之差，1.954¢，$[-19\space12⟩ - [-4\space4\space-1⟩ = [-15\space8\space1⟩$
• 升降差 $\frac{128}{125} = [7\space0\space-3⟩$
• 七限差 $\frac{225}{224} = 2^{-5} × 3^2 × 5^2 × 7^{-1} = [-5\space2\space2\space-1⟩$

等程律只用一行即可表示，其他調律需要多行。例如：四分折中律用純八、純五、正大三，映射表： $$ ⟨1\space1\space0]\ ⟨0\space1\space4] $$ 第一列：2/1 = 1 個純八度；第二列：3/1 = 1 個純八度 + 1 個純五；第三列：5/1 = 4 個純五。從左到右表示每個生程，從上到下表示該生程如何構成。