律曆初階上｜二：琴律學

一、品弦法

徽位

明確每箇徽位的位置是討論琴律的前提。七徽以下爲下準；四至七徽爲中準，比下準高一箇八度；四徽至一徽爲上準，比中準高一箇八度。「徽」表示徽法，「2 八」表示兩箇八度

一些簡單的計算舉例：

• 該弦散音弦長爲 1，則十徽八分近似： $\frac{3}{4} + (\frac{4}{5} - \frac{3}{4})/10 × 8 = \frac{79}{100}$
• 三弦散音弦長爲 1，則四弦十徽：$\frac{8}{9} × \frac{3}{4} = \frac{2}{3}$
• 使五弦十徽按音與三弦八徽按音同度，設五弦散音弦長爲 x，則 $\frac{3}{4} x = \frac{3}{5}, x = \frac{4}{5}$

古人製琴是怎麼確定徽位的？

• 折半爲七徽
• 七徽左右各折半，爲四、十徽
• 自四至岳，自十至龈，折半取中，爲一、十三徽
• 全長三分，爲五、九徽
• 自五至岳，自九至龈，折半取中，爲二、十二徽
• 全長五分，爲三、六、八、十一徽

常識：泛音音高

泛音音高是個很迷惑的問題，雖然非常簡單，但是琴人似乎都沒有一個相關說法，只好自己做實驗。首先可以確定的是，泛音都以 $\frac{1}{2}$ 對稱，弦長在 $\frac{1}{2}$ 以上的鏡像到 $\frac{1}{2}$ 以下。那麼現在依次來看：

• $\frac{1}{3}$ 五徽：點五徽彈，五、九徽不振。
• $\frac{1}{4}$ 四徽：點四徽彈，四、七、十徽不振。
• $\frac{1}{5}$ 三徽：點三徽彈，三、六、八、十一徽不振。
  • $\frac{2}{5}$ 六徽：點六徽彈，三、六、八、十一徽不振。實際振動長度只有 $\frac{1}{5}$，與三徽一致。
• $\frac{1}{6}$ 二徽：點二徽彈，五、七、九、十二徽不振。
• $\frac{1}{7}$ 暗徽一：
  • $\frac{2}{7}$ 和 $\frac{3}{7}$，實際振動長度爲 $\frac{1}{7}$。
• $\frac{1}{8}$ 一徽：
  • $\frac{2}{8}$ 四徽
  • $\frac{3}{8}$ 五.625 徽，實際振動長度爲 $\frac{1}{8}$ ，與一徽一致。
• $\frac{1}{9}$ 徽外：
  • $\frac{2}{9}$ 三.444 徽，實際振動長度爲 $\frac{1}{9}$。
• $\frac{1}{10}$ 徽外外：
  • $\frac{2}{10}$ 三徽
  • $\frac{3}{10}$ 四.6 徽，實際振動長度爲 $\frac{1}{10}$。
• 十一倍以上的就彈不出圓潤飽滿的泛音了，不能再用。

可以發現很明顯的規律：頻率比的分子不爲 1，且分子分母不能約分的，實際震動長度的分子爲 1，比如 $\frac{2}{5}$ 爲 $\frac{1}{5}$，$\frac{2}{7}$ 爲 $\frac{1}{7}$，而 $\frac{2}{6}$ 爲 $\frac{1}{3}$。

設計品弦法

下表是泛音、散按品弦法音程。準法僅用大全音、純四度、純五度、八度，徽法都可使用。知道弦式後，再參考此表，就可以很方便地想出泛音品弦法。例如一弦五徽 = 二弦六徽，一二弦音程就是徽小三度。

以泛泛和散按爲主，此外，去除與泛音法重複的音程與不成音的音程之後，還有三種按按品弦法。「低弦」「高弦」欄表示徽位，七徽以上都是泛泛，七徽以下都是按按或散按。

注：低弦 3=高弦 4，也可以等於低弦 6=高弦 7，雖然差了一個八度，但幾乎聽不出來。

比如現在給出側楚調的弦式一 6、二 1、三 3、四 ♯4、五 6、六 7、七 2，怎樣設計泛音品弦法？從二弦開始，6–1 是小三度，所以一弦 5 徽 = 二弦 6 徽；1–3 是大三度，所以二弦六徽 = 三弦七徽；一五弦是八度，所以一弦四徽 = 五弦七徽；6–2 是純四度，所以五弦四徽 = 七弦五徽；7–2 是小三度，所以六弦五徽 = 七弦六徽；♯4–6 是小三度，所以四弦五徽 = 五弦六徽。只要多嘗試幾次，就能找到合適的品弦法。

品弦法大全

正調品弦法默認爲宮調，其他四調對應如下。在用其他四調時一定要注意轉換，赫赫曆藏已經轉換好了。所以幽蘭用的宮調徽法一，陳長林說是純律二。

常用散按品弦法

古籍中一般都用散按品弦法，很少用泛音品弦法。下表中漢字數字表弦序，阿拉伯數字表徽位

二、律制對比

上文所說的「徽一」「徽二」指陳長林先生提出的「純律四種」，即徽法四種。下圖可與律學中的純律音系網對照看，這四種徽法就是音系網中各自截取一部分。

陳長林只說了商調純律二的品弦法，卽陳應時正調徽法品弦法，其他都沒說，我補充在品弦法中。下表比較五種律制的區別，根據各弦法泛音總結而來。音名相同而相差一個合音差的未計入，還需根據具體弦法律制來看。

陳長林只討論了七音。下根據對稱原則見 律學·五限純律·性能構建各律七音之外的其他偏音。

準法 徽法 都有大全音204¢、純四度498¢、純五度702¢。徽法還有特殊音程：小全音182¢，2–3、5–6、寬四度520¢，6–2、窄五度680¢，2–6。徽法的麻煩之處在於合音差的問題。其一、若品弦法不正確，那就天生帶有合音差；其二、犯調時可能會出現合音差，需要用同律同聲的按音來彌補。

準法 三分損益律 準法：三弦仲呂是黃鐘逆生 1 次而得，頻率比 4/3、498¢三弦五徽 = 一弦四徽。三分：順生 11 次的仲呂是 $\frac{177147}{131072}$、521.5¢，低了 23.5¢。卽三分損益法只能產生 ♯3，準法只能產生 4。準法還可以用純八度生律。

徽法 五限純律 基本相同，比如產生原理、音階、特殊音程。不同之處：純律用八度、純五度、大三度生律；徽法不僅用這些，還可用大六度5/3 八徽、純四度4/3 十徽、小三度6/5 十二徽按音直接生律，更爲簡便。另外，徽法在琴上可用任意徽位，旋宮轉調沒有困難。

複合律制 陳應時在一場講座中指出：

琴律不是复合律制。“复合律制”是由黄翔鹏先生提出的，它最早源出自杨荫浏先生所说的“二律并用”，就是指三分律与纯律同时在同器古琴上应用的一种律制。陈先生通过琴谱幽兰的调弦法及其散音、泛音、徽位按音、徽间按音等音律分析，指出琴谱幽兰所用的是纯律，而非纯律与三分律的“二律并用”。

試舉宮調神人暢爲例。若用準法，會產生純律音 ♯4；也可用徽法二。如果按陳應時先生所說，琴律不是複合的，那就只能用徽二品弦法。但是，爲何不能二律並用呢？

三、琴律計算器舉例

以下只是舉例，完整的直接在琴律計算器上算就可以，就不浪費紙了。

弦法

徽位音

泛音的徽位音一定包含於按音的徽位音。按音比泛音多的徽位：八、十、十二、十三徽。以正調爲例，按音多出來的是 9/10 二弦十徽、5/6 三弦十二徽、3/4 三弦十徽、20/27 四弦十二徽、5/9 六弦十二徽。

正調準法

正調徽法一

律內音

現在面臨的難題是，既然有五種律制，那麼這些徽位到底應該是多少啊？我又寫了一箇程序，思路是：先列出各調各律的各弦散音頻率比，比如宮調徽法一弦式 5 6 1 2 3 5 6，頻率比 3/4，5/6，1，9/8，5/4，3/2，5/3。 弦長比 = 1 / (各音頻率比 / 散音頻率比) = 散音頻率比 / 各音頻率比，再轉換成徽位就可以了。比如幽蘭商調徽法二，一弦爲宮：

前兩箇音是散勾一、十上半寸許勾二，可見二弦是九徽八分九，前兩箇音就是 1 5。爲何不是更常見的十徽呢？如果是，則爲 1·　5·，5 低了一箇合音差，而在徽法二中 1 5 是純五度。

13 箇調，每調 5 律，就是 65 張徽位表，不可能全印在紙上，直接用計算器算就好了。那麼接下來的腦洞就是，在琴面鋪上一層顯示屏，選擇弦法、律制，就可以在琴面上顯示這些線。

四、琴律史

小知識：準

「徽法」「準法」的名字是怎麼來的？徽是琴上的徽，徽法就是根據徽的位置來確定音高。準是用來的定音的工具，作用和律管、定音笛，或者現在的音叉差不多。準是京房發明的，京房說：

竹聲不可以度調，故作準以定數。準之狀如瑟，長丈而十三弦，隱間九尺，以應黃鐘之律九寸；中央一弦，下有畫分寸，以爲六十律清濁之節。後漢書律曆志

準的樣子像瑟，有柱來定各弦音高，弦下有刻度，標識十二律的位置。隱間就是岳山到龍齦的長度，風俗通說琴長四尺五寸，那麼準的長度就是琴的兩倍琴長可參考下徐理十則。1268 年徐理琴統琴準異同中國古代文獻集成第二輯，國家圖書館出版社，2011，頁 494–499：

準爲推律之器，而不宜制曲；而琴爲制曲之器，而不宜布律。曲固自律中來，然古人立法則不相爲用。準施柱，所以求同中之異；琴寘徽，所以求異中之同。準弦之下畫律十二，琴弦之旁寘徽十三。準之散弦十三，其聲如一，必施柱而後分高下，是律本不具於散弦之中；琴之散弦七，不待抑按，已有高下之別，是律已具於散弦之中。律不在散弦，故不得不施柱而登律於弦；律旣在散弦，則當就律定五音，不當律外求律，故曰琴非布律之器。此徽法、準法不相爲用一也。

琴各弦長度相同，而粗細鬆緊都不同，所以各弦音高不同；準各弦粗細鬆緊都一樣，於是需要加上柱來改變弦長，產生不同的音高。所以徐理說琴徽的作用是在不同的弦中求同音相合，而準線的作用是在相同的弦中求不同的音。

樸以謂十二律管互吹，難得其眞，乃依京房爲律準，以九尺之絃十三，依管長短寸分設柱，用七聲爲均，樂成而和。新五代史周臣傳王樸

琴徽的位置是根據純律來確定的；律管長度是由三分損益法算出的，準柱的位置由律管長短來確定，那麼準的刻度就是用三分損益法得來的，這就是徽法與準法區別的由來。徐理還說：

必欲使琴之用徽，則柱一無所用矣！不施柱可得爲準乎？必欲使琴如準之施柱，則徽一無所用矣！不用徽可得爲琴乎？此徽法、準法不相爲用二也。

這是在強調徽法與準法不可相容。

不過朱載堉說：

詳味京氏舊制，蓋謂準狀如琴，後人修史不達其旨，見云隱間九尺而十三弦，遂妄改爲瑟字。然彼書云：「中一弦下有畫，按畫以求諸律」，正猶琴之有徽，按徽以取聲耳，實未嘗言如瑟之有柱也。葛稚川西京雜記云：「咸陽宮中有琴，長六尺，安十三弦，三十六徽皆用七寶飾之⋯⋯」十三弦琴自古有之，京氏制準未必無據，是知漢志作「狀如瑟」者，蓋琴字之誤也。律學新說

朱載堉覺得瑟字是琴字之誤，不過王樸、徐理的材料非常清楚，準有柱，應該是瑟字無疑。至於十三弦琴，應該和準是兩碼事。

徽位說

• 陳拙天佑元年 904 年進士「上下暗徽」說明琴書大全輯陳拙琴籍，琴曲集成第五冊
• 崔遵度953–1020「天地自然之節」說琴書大全輯崔遵度琴箋
• 沈括「十三泛韻」說夢溪筆談補筆談
• 姜夔七弦琴圖說宋史樂志中華書局 1977 年，頁 3342
• 徐理十則1268 年徐理琴統，王耀華、方寶華主編：中國古代文獻集成第二輯，國家圖書館出版社，2012 年，頁 475─550
• 袁均哲太音大全集安徽法琴曲集成
• 朱載堉「琴徽論」律學新說

陳拙

夫聲之清濁大小相應，皆是明徽暗徽所生，故七弦應徽，所以取聲和也。除三十六徽外別有二暗徽。〔一徽〕至岳分五段，取近徽一段正，謂之上暗徽，名曰徽外，唯泛使之。十三徽至齦勻分五段，取近〔徽〕一段正，謂之下暗徽，亦名徽外，舉按泛聲使之。秋思弄中上暗徽上獨泛一聲，神人暢中上下暗徽上各泛一聲，兩譜泛聲皆名神授聲，幽館操中下暗徽上獨泛一聲。

可見暗徽在 $\frac{1}{10}$ 和 $\frac{9}{10}$ 處。

崔遵度

愚嘗病之，因張弓附按泛其弦，而十三徽聲具焉，況琴瑟之弦乎。是知所謂象者，蓋天地自然之節耳。

夫徽十三者蓋盡昭昭可聞者也，苟盡弦而考之，乃總有二十三徽焉，是一氣也。丈弦具之，尺弦亦具之，豈有長短大小之限哉。

沈括

所謂正聲者，如弦之有十三泛韻，此十二律自然之節也。盈丈之弦，其節亦十三；盈尺之弦，其節亦十三。故琴以爲十三徽。不獨弦如此，金石亦然。考工爲磬之法，已上則磨其端，已下則磨其旁，磨之至於擊而有韻處，即與徽應，過之則復無韻，又磨之至於有韻處，復應以一徽。石無大小，有韻處亦不過十三，猶弦之有十三泛聲也。此天地至理，人不能以毫釐損益其間。

崔遵度、沈括都意識到徽位是自然原理，而非人爲規定。

徐理

徐理十則卽將全弦長分爲兩分、三分，直到十分，卽一至十倍泛音，完整內容見附錄。去除重複的，共有 31 箇節點，前六則都是明徽，後四則爲暗徽。再參照音程表，徐理十則實際上是在五限純律基礎上加上了七限純律。

根據徐理十則，再考慮實際用途，我們可以記住一些七倍九倍十倍泛音特殊徽位。兩箇徽外：$\frac{1}{10}$、$\frac{9}{10}$ 純律小全音，$\frac{1}{9}$、$\frac{8}{9}$ 大全音，比較好找。

徽法正調品弦法

• 幽蘭弦法
• 廣陵散弦法
• 朱熹正調調弦法宋史樂志，中華書局，1977 年，頁 3344
• 姜夔「宮調」調弦法宋史樂志，頁 3342
• 陳敏子「正調」調弦法，琴律發微，琴曲集成第五冊
• 太音大全集「正調」徽法品弦法
• 風宣玄品「正調」調弦法
• 琴譜正傳西麓堂琴統「正調」調弦法
• 張鶴琴學入門

朱熹

朱熹與學者講定律之法：

十二律並用太史公九分寸法爲準，損益相生，分十二律及五聲，位置各定。按古人以吹管聲傳於琴上，如吹管起黃鍾，則以琴之黃鍾聲合之；聲合無差，然後以次徧合諸聲，則五聲皆正。唐人紀琴，先以管色合字定宮絃，乃以宮絃下生徵，徵上生商，上下相生，終於少商。下生者隔二絃、上生者隔一絃取之。凡絲聲皆當如此。今人苟簡，不復以管定聲，其高下出於臨時，非古法也。

朱熹認爲，正統的琴律應該用管色定音，而不是民間琴人所用的相對音高。又說了上生下生之法：隔一弦是上生徵生商等、純四度，隔二弦是下生宮生徵等、純五度。這源於沈括夢溪筆談：

如今之調弦，須先用管色合字定宮弦，乃以宮弦下生徵，徵上生商，上下相生，終於少商。凡下生者隔二弦，上生者隔一弦取之。

按：合字爲林鐘，一般三弦是仲呂。怎麼回事呢？朱熹又說：

調絃之法：散聲隔四而得二聲；中暉亦如之而得四聲；八暉隔三而得六聲；九暉按上者隔二而得四聲，按下者隔一而得五聲；十暉按上者隔一而得五聲，按下者隔二而得四聲。每疑七絃隔一調之，六絃皆應於第十暉，而第三絃獨於第十一暉調之乃應。及思而得之，七絃散聲爲五聲之正，而大絃十二律之位，又眾絃散聲之所取正也。故逐絃之五聲皆自東而西，相爲次第。

他發現的問題是六條弦都是應於十徽，只有三弦是應於十一徽，但沒解釋原因。不過「二聲」「四聲」「六聲」什麼意思呢？

其六絃會於十暉，則一與三者，角與散角應也；二與四者，徵與散徵應也；四與六者，宮與散少宮應也；五與七者，商與散少商應也；其第三、第五絃會於十一暉，則羽與散羽應也。義各有當，初不相須，故不同會於一暉也。

已知一弦，一 10 = 三散純四，三 11 = 五散徽大三，五 10 = 七散純四，一弦與六弦爲八度，四 10 = 六散，二 10 = 四散。可得各弦頻率比爲 一 1 二 9/8 三 4/3 四 3/2 五 5/3 六 2 七 20/9。朱熹法得出的二弦高了一箇合音差，最後還需要用二弦與七弦相應。

姜夔

宋志引用姜夔七絃琴圖說：

絃有七有九，實即五絃。七絃倍其二，九絃倍其四，所用者五音，亦不以二變爲散聲也。或欲以七絃配五音二變，以餘兩絃爲倍，若七絃分配七音，則是今之十四絃也。聲律訣云：『琴瑟齪四者，律法上下相生也。』若加二變，則於律法不諧矣。或曰：『如此則琴無二變之聲乎？』曰：『附木取之，二變之聲固在也。』合五七九絃琴，總述取應聲法，分十二律十二均，每聲取絃暉之應，皆以次列按。

不論是七弦琴還是九弦琴，其實都是五弦，七弦是高一箇八度，九弦是高兩箇八度；另一種方法是七弦配七音，八九弦高一箇八度。

七絃散而扣之，則間一絃於第十暉取應聲。假如宮調，五絃十暉應七絃散聲，四絃十暉應六絃散聲，二絃十暉應四絃散聲，大絃十暉應三絃散聲，惟三絃獨退一暉，於十一暉應五絃散聲，古今無知之者。

姜夔品弦法與朱熹很相似，只是順序不同。已知七弦，五 10 = 七散，三 11 = 五三，一 10 = 三散，二七爲八度，二 10 = 四散，四 10 = 六散。假設七弦頻率 20/9，則五弦 5/3，三弦 4/3，一弦 1，六弦 10/9，四弦 40/27，六弦 160/81，低了合音差，且四七弦 2–6 不是窄五度，而是純五度。

陳敏子

1320 年琴律發微記載了一種當時流行的兩種正調品弦法琴曲集成第五冊，1980，頁 136。

姑以仲呂宮言之，
世用徽，凡調弦第三弦應五弦散聲爲角，在十一徽之上；琴律徽則其應正在十一徽。
世用徽，第一弦應第三弦散聲爲仲呂宮，在十徽之上；琴律徽則仲呂正與十徽相對。
世用徽，第三弦應第二弦散聲爲羽，在八徽之上；琴律徽則其應正在八徽。
皆不必求之各徽上，甚爲整齊，並無毫髮參差處。

「世用徽」卽準法，「琴律徽」卽徽法。徽法品弦法，已知三弦仲呂爲宮，三 11 = 五散，一 10 = 三散，二 8 = 三散。可得三弦 1，一弦 3/4，二弦 5/6，五弦 5/4。

準法正調品弦法

沈括

沈括補筆談：

隔二弦鼓之，皆與九徽應，獨徵聲與十徽應，此皆隔兩律法也。⋯⋯故鼓之六與一應，七與二應，皆不失本律之聲。

按照隔一弦或者隔二弦的方法，可得：

• 一 10 = 三散，二 10 = 四散，四 10 = 六散，五 10 = 七散
• 一 9 = 四散，二 9 = 五散，三 9 = 六散，四 9 = 七散

朱熹

朱熹琴律說：

沈氏以隔二者爲下生，隔一者爲上生。蓋九徽之宮，隔二者下生散徵，而散徵隔一上生十徽之商；九徽之商隔二下生散羽，而散羽隔一上生十一徽之角；九徽之角，隔二下生散少宮，而散少宮隔一上生十徽之徵；九徽之徵隔二下生散少商，而散少商隔一上生十徽之羽也。

已知一弦，一 9 = 四散，二 10 = 四散，二 9 = 五散，三 10.8 = 五散，三 9 = 六散，四 10 = 六散，四 9 = 七散，五 10 = 七散

徽準交替

準法與徽法在琴史發展中有較複雜的關係。宋代之前大多採用徽法。沈括提出準法品弦法。南宋徐理琴統、元陳敏子琴律發微區分了徽法「琴律徽」、準法「世用徽」，不讚成使用準法，可見元代就已經流行準法了。西麓堂發現了徽法與準法的矛盾，使正調定弦合于準法，朱載堉提倡準法品弦法，創作大量準法品弦曲，但記譜仍採用徽法。直到 1614 嚴天池松弦館琴譜纔開始使用準法徽分記譜法，只是未全面應用，1673 徐青山大還閣琴譜開始全面應用，把十一徽改爲十徽八分，八徽改爲七徽九分，另配以八徽半、七徽六分、七徽三分、六徽七分、六徽半、六徽二分、五徽六分、四徽八分、四徽六分、四徽四分、四徽二分等種種準法徽間按音，形成一整套準法定弦、轉調、記譜的琴律體系，沿用至今。需要注意的是，這種徽分記譜法和已有的徽法徽間記譜法是兩箇體系。

在徽準交替過程中，使用準法的琴家卻依然用徽法的方法來轉調，造成音律混亂。十徽–十一徽相差 112¢，然而準法 3–4、7–1 都是 90¢，這一錯誤在 1821 王仲舒指法匯參確解已有糾正。具體方法參考散按品弦法

五、展望

菱法的提出

所有徽位泛音唯獨缺七倍泛音，我們可以補上，這實際上是徐理十則就已經提出的長度，七倍徽位用菱形 ◆ 標識。用「菱 1」「菱 2」來指代 $\frac{1}{7}$、$\frac{2}{7}$ 的徽位，六菱的泛音音高全都相同。根據「準法」「徽法」的命名習慣，我們將這種律制命爲「菱法」，卽七限純律在琴上的運用。下表爲各菱具體位置、按音音程。

下表爲菱法律的泛音品弦法。

♭3 和菱法 ♯2 可根據具體情況選擇，♭6 可用菱法 ♯5 替換，徽法 ♯2 ♯4 可用菱法代替。這是把所有弦法統合而言，使用時還需根據各弦法具體情況而定。菱法還有些更緊張的音程未列出，也需根據具體情況選擇。

琴律與琴調的貫通

许云珩 ：

或许在中国音乐中“三音列”“三个骨干”会更合适，譬如宫角羽，羽宫角等等。那么不同的纯律音阶就存在不同的和谐音列，构成一定的互补关系，譬如相对常用的纯律一中 2 4 6 不和谐，更常用于古琴商调的纯律二则 5 7 2 不和谐。举例言之，黄钟调紧五慢一的许多曲子如秋月照茅亭、大胡笳，都用到了夹钟一律设一弦为无射〔瀚案：一弦爲 1，夾鐘爲 4〕，且在眞·商调倾向的时候作较大的用场，那么 2 4 6 不谐的纯律一调弦就不能够担纲。古琴商调一弦为黄钟的情况下也有类似的事件，要保证 2 4 6 的和谐。纯律三四则是完全互补，前者 6 1 3、4 6 1、2 4 6 不谐，后者 1 3 5、3 5 7、5 7 2 不谐，则前者容易弹大调而后者适宜凄迷瑰丽的 minor如离骚、潇湘。

⋯⋯而在纯律逐渐淡出后，这种模式也逐渐变为了用五度关系做主属音的，譬如羽角、宫徵。以列子御风为例，本身角调是煞于宫音的，是常用宫角音程，兼取羽音多一般宫调则常用宫徵，在明代中后期，不再用宫 - 角关系调弦，原先的宫角合声和宫角音程打圆都变成了羽 - 角或角 - 角，也就从三音列转为了主音属音，虽然它仍然收束于宫，但是其调性相比早期是模糊了不少的。

或许在早期琴曲上，采用这个三音列的视角能够理解为什么某个曲子乃至某种调性用某种纯律音阶，相对于单纯的分析 F 宫 D 羽之类的更加有现实意义，更贴近谱本展现的音程关系的同时也和西乐更易沟通。

依次檢査一下划掉的表示不和諧。純律一：

• 2 4 6 F/D = 32/27 畢氏小三；A/F = 5/4 正大三；A/D = 40/27 純律窄五
• 5 7 2 D/B = 6/5 正小三；B/G = 5/4 正大三；D/G = 純五

純律二：

• 2 4 6 F/D = 正小三；A/F = 正大三；A/D = 純五
• 5 7 2 D/B = 畢氏小三；B/G = 正大三；D/G = 純律窄五

純律三：

• 6 1 3 C/A = 畢氏小三；E/C = 正大三；E/A = 純律窄五
• 4 6 1 C/A = 畢氏小三；A/F = 81/64 畢氏大三；C/F = 純五
• 2 4 6 F/D = 畢氏小三；A/F = 畢氏大三；A/D = 純五
• 1 3 5 E/C = 正大三；G/E = 正小三；G/C = 純五
• 3 5 7 G/E = 正小三；B/G = 正大三；B/E = 純五
• 5 7 2 B/G = 正大三；D/B = 正小三；D/G = 純五

純律四則反之。

附錄

「寸許」

幽蘭文字譜說的「寸許」到底是多少呢？陳應時頁 181

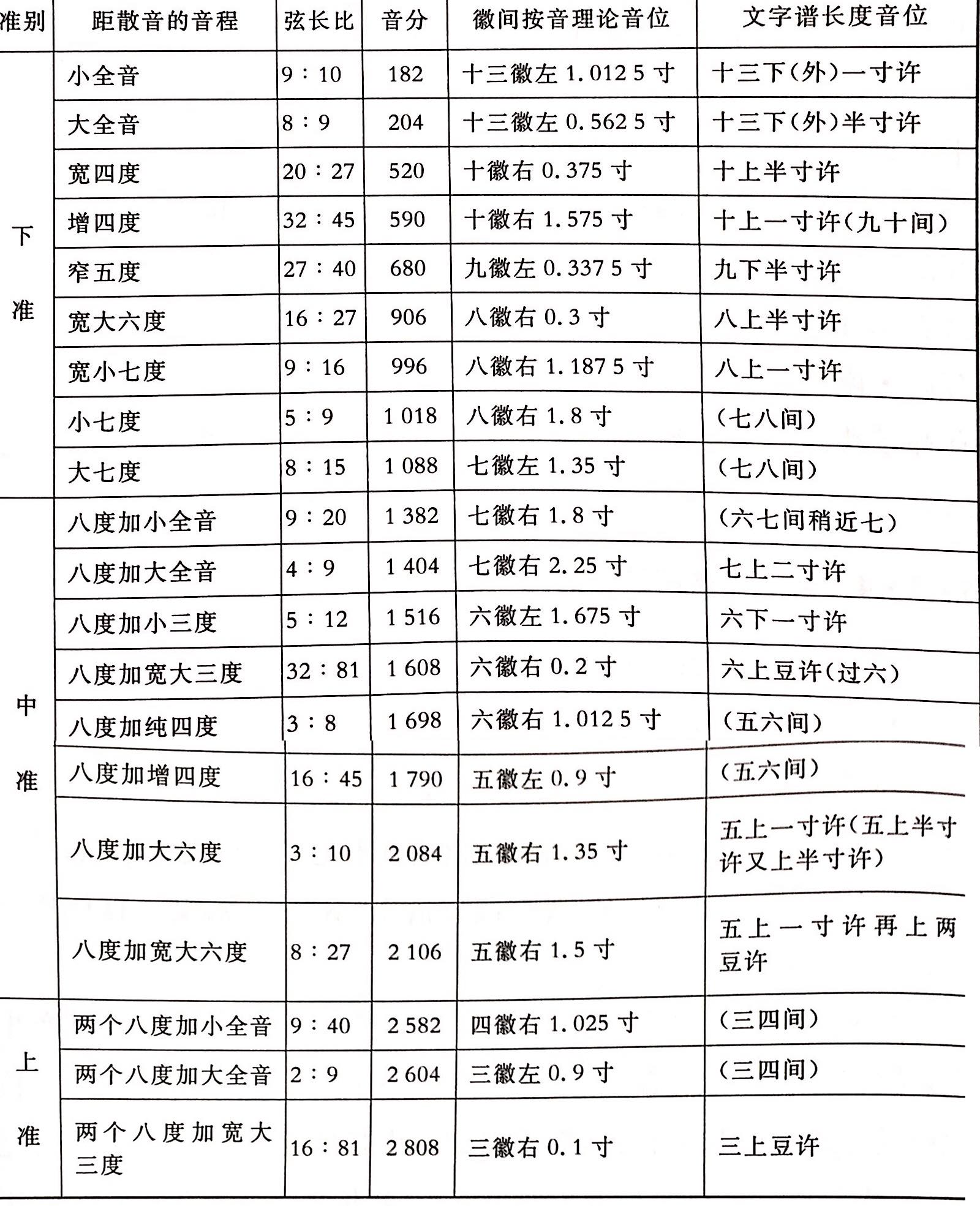
徐理十則

• 一則
  • 弦間之長四尺五寸。
  • 按黃鐘之長九寸，伸爲九尺，半爲四尺五寸。法用古尺，較之浙尺，長於古尺一寸八分。今太史局土圭測景尺，乃東京遺法，或云即是黍尺，亦云周尺，參之琴工尺法，大率相似。或云神農琴長三尺六寸六分，此蓋前人推考尺法失實致此。今從朱文公訂定之法，以四尺五寸爲正。
• 二則
  • 二而分之，各得二尺二寸五分。
  • 中節爲七徽，按聲、泛聲與散聲同，是謂中聲。
• 三則
  • 三而分之，各得一尺五寸。
  • 一節如上數，爲五徽，有隔一下應，隔二上應，泛聲亦有應。
  • 二節三尺，爲九徽，有隔二上應，泛聲亦有應。
• 四則
  • 四而分之，各得一尺一寸二分五釐。
  • 一節如上數，爲四徽，泛聲有應。
  • 二節二尺二寸五分，同七徽。
  • 三節三尺三寸七分五釐，爲十徽，有隔一上應，泛聲亦有應。
• 五則
  • 五而分之，各得九寸。
  • 一節如上數，爲三徽，有隔一上應。
  • 二節一尺八寸，爲六徽，有隔一上應，泛聲亦有應。
  • 三節二尺七寸，如八徽，有並弦下應，隔三上應，泛聲亦有應。
  • 四節三尺六寸，爲十一徽，有隔一上應，泛聲亦有應。
• 六則
  • 六而分之，各得七寸五分。
  • 一節如上數，爲二徽，有隔一下應，泛聲亦有應。
  • 二節一尺五寸，同五徽。
  • 三節二尺二寸五分，同七徽。
  • 四節三尺，同九徽。
  • 五節三尺七寸五分，爲十二徽，有並弦上應，泛聲亦有應。
• 七則
  • 七而分之，各得六寸四分二釐八毫餘四。
  • 一節如上數，居一二徽之間，有並弦下應。
  • 二節一尺二寸八分五釐六毫，居四五徽之間，有隔三上應，並弦下應。
  • 三節一尺九寸二分八釐四毫，居六徽之下，有隔三下應，並弦上應。
  • 四節二尺五寸七分一釐二毫，居八徽之上，有並弦下應，隔三上應。
  • 五節三尺二寸一分四釐，居九十徽之間，外雜調，有隔一上應，隔二下應。
  • 六節三尺八寸五分六釐八毫，居十二、十三徽之間，有並弦上應。
• 八則
  • 八而分之，各得五寸六分二釐五毫。
  • 一節如上數，爲一徽，有隔一上應，泛聲亦有應。
  • 二節一尺一寸二分五釐，同四徽。
  • 三節一尺六寸八分七釐五毫，居五六徽之間，有隔二下應，隔一上應。
  • 四節二尺二寸五分，同七徽。
  • 五節二尺八寸一分二釐五毫，居八九徽之間，有隔一下應，隔二上應。
  • 六節三尺三寸七分五釐，同十徽。
  • 七節三尺九寸三分七釐五毫爲十三徽，泛聲有應。
• 九則
  • 九而分之各得五寸。
  • 一節如上數，居一徽之上，有並弦下應。
  • 二節一尺，居三、四徽之問，有並弦上應。
  • 三節一尺五寸，同五徽。
  • 四節二尺，居六七徽之間，有隔三下應，並弦上應
  • 五節二尺五寸，居七八徽之間，變宮、變徵聲在此。
  • 六節三尺，同九徽。
  • 七節三尺五寸，居十徽、十一徽之間，無應。
  • 八節四尺，居十三徽之外，有並弦上應。
• 十則
  • 十而分之，各得四寸五分。
  • 一節如上數。此一徽上之遠者，有隔一上應。
  • 二節九寸，同三徽。
  • 三節一尺三寸五分，居五徽之上，有並弦下應，隔三上應。
  • 四節一尺八寸，同六徽。
  • 五節二尺二寸五分，同七徽。
  • 六節二尺七寸，同八徽。
  • 七節三尺一寸五分，居九徽之下，外調有隔一下應。
  • 八節三尺六寸，同十一徽。
  • 九節四尺五分。此徽外之遠育者，有並弦上應。

陳應時琴律學勘誤

@ 清泓：两处不可略过的错误，2021-01-19

其一，159 頁【章 3·6·2 徽法正弄調的徽位按音】表 3-28

若以正調三弦爲下宮音，則二弦七徵按音當是下羽，而此頁表格關於二弦一行竟填为羽等，有誤。

其二，108 页【章 3·4 徽法“正弄调”转弦换调法】清角为宫

讲到“清角为宫”时，書中以正調散角音與羽音弦十徽按音同聲相應，以正調轉蕤賓調，動緊正調角音弦五弦使之應正調羽音弦十一徽七弦。此處有兩誤一憾。

凡兩弦散按相應於九徽十徽者除宮音弦之十徽下移十一徽／十徽八分外，皆是上散隔一下按九。无有兩弦隔一相應，在外者散在內者取十徽者。除非是下散隔一上應十。此一誤。

旣是要清角爲宮，若用按法調弦，正調角音弦五弦散音應宮音弦三弦十一徽，緊五弦使與三弦十徽應，然後得蕤賓宮；若定要用正調羽音弦七弦當從散五弦應七弦九徽變爲應七弦八徽半，緊五弦。此二誤。

若以十一徽有二分之猶疑、八徽半有指分之不均，則亦可用泛調定。緊正調五弦，使之泛五徽與泛正調三弦四徽應。泛法不涉分度而易爲，按法轉調不免有度數左右，有失之差釐之憂而下指猶疑聲滯之病生。變宮爲角與清角爲宮皆有此簡易法，不出三五弦間而得。然书中未及，此一憾。

所用本子：2015 年 12 月第二次印刷版